Trong toán học, đặc biệt là đối với các bài toán liên quan đến hình học và đại số, bảng công thức lượng giác là một tài nguyên không thể thiếu. Học sinh sẽ dễ dàng áp dụng bảng công thức này. Chúng tôi sẽ đi sâu vào bảng công thức lượng giác trong bài viết này, từ các công thức cơ bản đến các ứng dụng thực tế của nó. Chúng tôi cũng sẽ nói về cách học thuộc hiệu quả nhất trong 40 phút.
1.Giới thiệu về bảng công thức lượng giác
Bảng công thức lượng giác không chỉ là một danh sách các công thức mà còn có rất nhiều ứng dụng và lý thuyết. Nó đưa ra những định lý và quy luật đầy sức mạnh mà mọi người đều cần nắm vững vì nó giúp chúng ta nhận thức được mối liên hệ giữa các góc và độ dài cạnh của một tam giác.
- Từ hình học đến đại số, từ giải tích đến thống kê, bảng công thức lượng giác là một phần quan trọng của toán học. Một số nội dung chính mà chúng tôi sẽ giới thiệu trong phần này được liệt kê dưới đây.
Ý tưởng về lượng giác
- Một lĩnh vực toán học được gọi là lượng giác nghiên cứu mối quan hệ giữa các cạnh và góc của một tam giác. Đặc biệt, nó nói về tam giác vuông, nơi các quy tắc lượng giác được sử dụng phổ biến. Các hàm số lượng giác như sin, cos, tan, cot, sec và csc đã được sử dụng để tính toán và phân tích.
- Những hàm số này không chỉ được tìm thấy trong các bài toán cơ bản mà còn trong nhiều lĩnh vực khác, chẳng hạn như kỹ thuật, vật lý và thậm chí khoa học xã hội. Điều này chứng minh tính ứng dụng và đa dạng của chúng.
Bảng công thức lượng giác
- Bảng công thức lượng giác quan trọng vì chúng giúp bạn tiết kiệm thời gian khi giải bài tập và giúp bạn hiểu toán học tốt hơn. Khi bạn biết cách áp dụng các bảng công thức vào các bài toán cụ thể, bạn sẽ cải thiện khả năng tư duy logic của mình.
- Bảng công thức cũng quan trọng đối với việc xây dựng nền tảng vững chắc cho các khái niệm nâng cao. Việc làm quen với bảng công thức lượng giác sẽ cực kỳ có lợi nếu bạn muốn tiếp cận các lĩnh vực liên quan như giải tích hoặc hình học không gian.
2.Các công thức cơ bản trong bảng công thức lượng giác
Mặc dù có nhiều công thức trên bảng công thức lượng giác, nhưng đây là một số công thức cơ bản mà mọi người nên biết. Các bài toán liên quan đến lượng giác sẽ yêu cầu các công thức này.
Công thức hàm cho tổng số giác
Một số hàm số lượng giác cơ bản là:
- Sin, còn được gọi là sinus, là tỷ lệ giữa cạnh huyền và cạnh đối diện trong tam giác vuông.
- Cos, còn được gọi là cosinus, là tỷ lệ giữa cạnh huyền và cạnh kề trong tam giác vuông.
- Tan, còn được gọi là tan, là tỷ lệ giữa cạnh đối diện và cạnh kề.
- Ngoài ra, các hàm ngược, chẳng hạn như cosec (csc), sec (sec) và cot (cot), cũng có sẵn. Bạn sẽ thành thạo hầu hết các bài toán lượng giác nếu sử dụng những hàm này đúng cách.
Công thức cộng và tác động
- Bên cạnh hàm số lượng giác, chúng ta cũng cần hiểu các công thức cộng và hiệu. Đây là những công thức tính toán và biến đổi rất quan trọng.
- Trong công thức cộng, sin(a + b) tương đương với sin(a)cos(b) và cos(a)sin(b).
- Công thức hiệu cho thấy sin(a – b) tương đương với sin(a)cos(b) và cos(a)sin(b).
- Nhiều bài toán phức tạp hơn có thể được giải được với sự trợ giúp của các công thức này, đặc biệt là khi xử lý các góc không phải là góc đặc biệt.
Công thức nhân đôi và bán kính cũng rất quan trọng:
- Công thức nhân đôi cho thấy rằng sin(2a) = 2sin(a)cos(a).
- Công thức bán kính cho thấy rằng sin2(a) + cos2(a) = 1.
- Bạn sẽ có cái nhìn tổng quát hơn về các mối quan hệ giữa các hàm lượng giác nếu bạn sử dụng những công thức này.

3.Ứng dụng của bảng công thức lượng giác trong toán học
Bảng công thức lượng giác không chỉ là một phần quan trọng của bài kiểm tra mà còn là một phương tiện hữu ích trong nhiều lĩnh vực. Bảng công thức lượng giác được sử dụng cho các mục sau.
Giải quyết bài toán bằng cách sử dụng hình học
- Bảng công thức lượng giác được sử dụng phổ biến nhất trong hình học, đặc biệt là trong các lĩnh vực liên quan đến tam giác. Các công thức có thể được sử dụng để xác định cạnh hoặc góc chưa biết của tam giác và sau đó xác định diện tích hoặc chu vi của nó.
- Ví dụ, nếu bạn biết độ dài của hai cạnh của một tam giác vuông, bạn có thể dễ dàng tìm được góc của nó bằng cách sử dụng hàm số tan. Mặt khác, nếu bạn biết một góc và một cạnh, bạn sẽ có thể tính toán được các góc và cạnh còn lại.
Ứng dụng trong lĩnh vực vật lý
- Vật lý thường sử dụng bảng công thức lượng giác để giải thích các chuyển động sóng, dao động và nhiều hiện tượng khác. Các hàm lượng giác như sin và cos thường được tìm thấy trong các phương trình chuyển động, giúp mô tả chính xác hành vi của các vật thể.
- Ngoài ra, các nhà khoa học thường sử dụng bảng công thức lượng giác để phân tích tần số và biên độ của sóng khi nghiên cứu âm thanh và ánh sáng. Điều này cho thấy rằng toán học liên quan đến nhiều lĩnh vực khoa học khác nhau.
Phân tích thông tin
- Bảng công thức lượng giác cũng được sử dụng trong thống kê. Để đưa ra những kết luận đáng tin cậy, bạn có thể xác định các mẫu trong dữ liệu bằng cách sử dụng các công thức lượng giác.
- Chẳng hạn, trong phân tích hồi quy, bạn có thể tối ưu hóa mô hình dự đoán bằng cách tìm ra mối quan hệ giữa các biến số bằng cách sử dụng các hàm số lượng giác.
4.Lịch sử phát triển của bảng công thức lượng giác
Lịch sử thú vị và phong phú của bảng công thức lượng giác cho thấy sự phát triển của toán học và khoa học tự nhiên trong nhiều thế kỷ.
nguồn gốc của lượng giác
- Lượng giác lần đầu tiên được sử dụng tại Babylon cổ đại, nơi các nhà khoa học đã bắt đầu xem xét các mối quan hệ giữa các cạnh và góc trong tam giác để phục vụ cho việc đo đạc diện tích đất đai. Các nhà toán học Hy Lạp như Hipparchus và Ptolemy đã ghi nhận phương pháp này đã phát triển dần theo thời gian.
- Họ đã tạo ra bảng công thức lượng giác bao gồm các giá trị cho các góc riêng biệt. Điều này đã đặt nền móng cho việc sử dụng các hàm số lượng giác sau này.
Sự phát triển của các công thức liên quan đến lượng giác
- Nhiều nhà toán học trong thời kỳ phục hưng, bao gồm Newton và Descartes, đã tiếp tục nghiên cứu và mở rộng các công thức lượng giác. Họ phát triển các công thức cho các quan điểm tổng quát hơn cũng như các quan điểm đặc biệt.
- Sự phát triển này đã dẫn đến sự phát triển của bảng công thức lượng giác hiện tại, có nhiều công thức đa dạng và phong phú.
Bảng công thức lượng giác ảnh hưởng đến các lĩnh vực khác
- Bảng công thức lượng giác có tác động đáng kể đến toán học và nhiều lĩnh vực khác, chẳng hạn như kỹ thuật, vật lý, thiên văn học và địa lý. Với sự phát triển của máy tính và các công nghệ hiện đại, các công thức lượng giác đã trở nên phổ biến hơn và có nhiều ứng dụng hơn.
- Ngày nay, bảng công thức lượng giác đã trở thành một phần quan trọng của giáo dục và nghiên cứu khoa học.
- biết ngày hôm nay, với nhiều công thức phong phú và đa dạng.
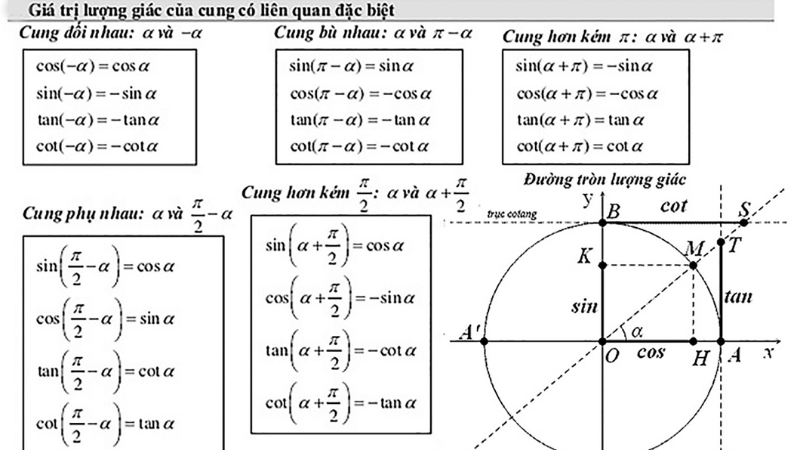
5.Ảnh hưởng của bảng công thức lượng giác đến các lĩnh vực khác
Việc thực hành là rất quan trọng để nắm vững bảng công thức lượng giác. Để củng cố kiến thức và kỹ năng, chúng ta sẽ cùng xem xét một số bài tập thực hành dưới đây.
Bài tập đầu tiên
- Việc tính toán các giá trị của hàm lượng giác thường là chủ đề của các bài tập cơ bản. Bạn có thể thử các bài tập như tính giá trị sin, cos và tan cho các góc như 0, 30, 45, 60 và 90 độ.
- Giải quyết các bài toán đơn giản về tam giác vuông như tính độ dài cạnh hoặc diện tích.
Bài tập được cải thiện
- Bạn có thể tiến tới các bài tập nâng cao hơn sau khi nắm vững các bài tập cơ bản. Những bài tập này thường yêu cầu sử dụng nhiều công thức khác nhau.
- Định lý sin và cos được sử dụng để tìm mối quan hệ giữa các góc của tam giác không vuông.
- Ứng dụng hàm lượng giác để giải quyết các bài toán liên quan đến chuyển động sóng và dao động.
Ứng dụng trong thực tế
- Cuối cùng, bạn nên áp dụng kiến thức đã học vào thực tế để cải thiện khả năng sử dụng bảng công thức lượng giác. Bạn có thể tham gia vào các dự án khoa học sáng tạo, thiết kế công trình hoặc khảo sát địa hình.
- Bạn sẽ cảm nhận rõ hơn giá trị của bảng công thức lượng giác trong đời sống hàng ngày nếu bạn áp dụng nó vào thực tế.
6.Những lưu ý khi sử dụng bảng công thức lượng giác
Bảng công thức lượng giác là một công cụ tuyệt vời, nhưng có nhiều điều cần lưu ý khi sử dụng nó. Đây là một số lời khuyên để sử dụng bảng công thức hiệu quả nhất.
Hiểu tất cả các công thức.
- Đảm bảo rằng bạn hiểu rõ từng công thức và cách chúng hoạt động trước khi bắt đầu sử dụng bảng công thức. Khi gặp phải các bài toán phức tạp, việc chỉ học thuộc lòng mà không hiểu sâu có thể dẫn đến tình trạng lúng túng.
- Thay vì chỉ ghi nhớ, hãy cố gắng khám phá nguồn gốc của mỗi công thức và lý do đằng sau nó. Điều này sẽ cho phép bạn có cái nhìn tổng quát hơn và sẽ dễ dàng áp dụng vào thực tế.
Tìm hiểu các công thức.
- Kiểm tra lại các công thức mà bạn đã học là một điều nữa rất quan trọng. Sự quên lãng là bình thường, và việc rà soát lại kiến thức sẽ giúp cải thiện trí nhớ.
- Điều này có thể được thực hiện bằng cách làm bài tập hoặc thậm chí tạo ra một bảng công thức để tham khảo.
Đừng ngần ngại hỏi.
- Cuối cùng, nếu bạn gặp khó khăn trong việc hiểu hoặc áp dụng bảng công thức, hãy nói với những người bạn quan tâm. Có thể là bạn bè, giáo viên hoặc những người có kinh nghiệm trong lĩnh vực. Họ có thể cung cấp những giải thích và góc nhìn hữu ích để giúp bạn vượt qua những vấn đề.
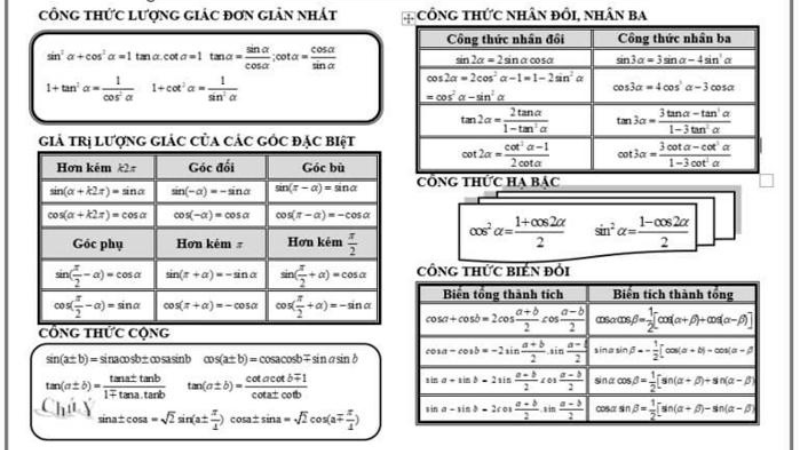
7.Kết quả:
Bảng công thức lượng giác là một phần quan trọng của quá trình học toán. Bên cạnh việc cung cấp các công thức cơ bản, nó còn có nhiều ứng dụng thực tiễn mà bạn có thể tìm thấy trong cuộc sống hàng ngày.
Sau khi đọc bài viết này, tôi hy vọng rằng nó đã giúp bạn hiểu rõ hơn về bảng công thức lượng giác, từ lý thuyết đến thực tiễn. Bạn sẽ thành công trong học tập và cuộc sống nếu bạn dành thời gian để học tập và áp dụng kiến thức này. Bạn có thể tìm hiểu thêm về công thức cấp số cộng, cũng rất quan trọng. Trên đây là bài viết về bảng công thức lượng giác , chi tiết xin truy cập website: congthucluonggiac.net xin cảm ơn!
