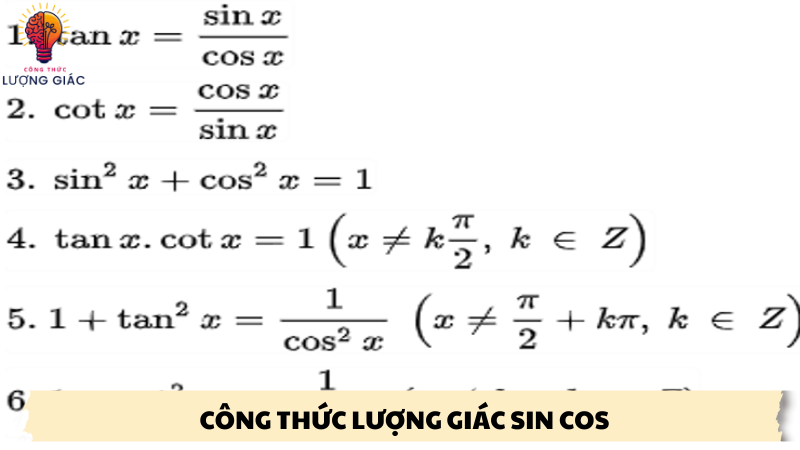Trong học toán, khái niệm “công thức lượng giác sin cos” là cần thiết để mô tả và giải các bài toán liên quan đến các góc và tam giác . Những công thức này có nhiều ứng dụng ngoài toán học trong nhiều lĩnh vực khác nhau, coi hạn như kỹ thuật, vật lý, khoa học máy tính và thậm chí cả chí trong cuộc sống hàng ngày.
1. Công thức lượng giác cơ bản về sin và cos
Phương pháp toán học được gọi là công thức giác giác mô tả mối liên hệ giữa các hàm giác giác như sin , cos , tan , cot, sec và csc. Hai hàm số quan trọng nhất trong đó là sin (sine) và cos (cosine).
Ý nghĩa hình học của hàm số sin và cos
- tọa độ y của điểm trên đơn vị đường tròn mà góc với trục x là x là hàm sin (x) của góc x tính bằng radian.
- tọa độ x của điểm trên đơn vị đường tròn mà góc với trục x là x là hàm số cos(x) của góc x tính bằng radian.
- Điều này có nghĩa là sin(x) và cos ( x) là góc độ y và góc x nếu một điểm được vẽ trên đường tròn đó .
Các giá trị cơ bản của sin và cos
- Cơ sở giá trị của sin và cos có thể được tính toán bằng cách sử dụng các góc đặc biệt như 0, π/6, π/4, π/3 và π/2:
- Để hiểu và nhớ các công thức lượng giác khác, sin(π/6) = 1/2, cos(π/6) = √3/2, sin(π/4) = √2/2, cos(π/4) = √2/2, sin(π/3) = √3/2, cos(π/3) = 1/2, sin(π/2) = 1, cos(π/2) = 0.
2. Các công thức biến đổi giữa sin và cos
Các công thức lượng giác không chỉ cung cấp các giá trị cơ bản mà còn cho phép biến đổi giữa các hàm số sin và cos. Điều này rất hữu ích khi giải quyết các bài toán có liên quan .
Công thức Pytago-rơ
- Công thức Pytago-rơ, còn được gọi là công thức Pytago, là một trong những công thức quan trọng nhất liên quan đến sin và cos:
- Công thức sin2(x) + cos2(x) =1
- Theo công thức này, bình phương của sin(x) cộng với cos(x) luôn bằng 1. Khi bạn chỉ biết sin và cos, điều này rất hữu ích để tính toán chúng.
Công thức biến đổi giữa sin và cos
Ngoài ra, chúng ta có thể dễ dàng thay đổi sin(x) và cos(x) với các công thức sau:
- sin(x) tương đương với cos(π/2 – x).
- Giá trị của cos(x) bằng sin(π/2 – x).
- Khi giải quyết các bài toán tam giác hoặc tính toán các góc bổ sung, các công thức này cho phép chuyển đổi giữa sin và cos.
Ý nghĩa hình học của công thức lượng giác sin cos
- Công thức lượng giác sin cos không chỉ có ý nghĩa toán học mà còn có ý nghĩa hình học. Hiểu hình học sẽ giúp chúng ta hiểu và vận dụng các khái niệm lượng giác.
- Bằng sin và cos, biểu diễn tam giác vuông
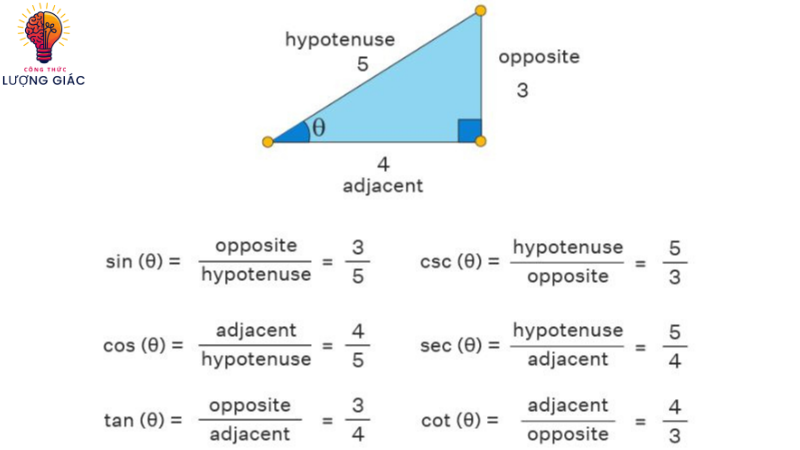
- Sin và cos có thể được sử dụng để mô tả các tam giác vuông. Về cụ thể:
- Nếu một tam giác vuông có cạnh kề a, cạnh đối b và góc nhọn θ
- sin(θ) = b/c
- cos(θ) = a/c Trong đó c là cạnh huyền của tam giác.
- Điều này cho phép tính toán các cạnh và góc của tam giác vuông với ít dữ liệu.
Biểu diễn vị trí trên đơn vị đường tròn bằng sin và cos
Như đã đề cập, sin và cos cũng có thể được sử dụng để biểu diễn vị trí của một điểm trên đơn vị đường tròn. Về cụ thể:
- Tọa độ của điểm P trên đơn vị đường tròn với góc của đường thẳng OP là θ là (cos(θ), sin(θ).
- Do đó, sin và cos không chỉ có ý nghĩa toán học mà còn có ý nghĩa hình học, vì chúng cho phép chúng ta hình dung và mô tả các đối tượng hình học.
3. Ứng dụng của công thức lượng giác sin cos trong giải toán
Công thức lượng giác sin cos có nhiều ứng dụng thực tế, đặc biệt là trong việc giải quyết các bài toán về tam giác và góc.
Giải tam giác
- Công thức lượng giác rất quan trọng để giải quyết các bài toán tam giác. Chúng ta có thể sử dụng các công thức lượng giác để tính toán các thông tin còn lại khi chúng ta có thông tin về một tam giác, chẳng hạn như độ dài cạnh hoặc góc của nó.
- Ví dụ, chúng ta có thể sử dụng công thức lượng giác để tính độ dài của cạnh thứ ba hoặc các góc còn lại của tam giác nếu chúng ta biết độ dài của hai cạnh và góc lại giữa chúng.
Tính khoảng cách và độ cao
- Các công thức lượng giác sin cos cũng được sử dụng rộng rãi để tìm khoảng cách và độ cao. Ví dụ, chúng ta có thể sử dụng công thức lượng giác để tính khoảng cách đến một vật thể khi chúng ta biết độ cao của nó và góc quan sát của nó.
- Tính toán khoảng cách và độ cao có thể được sử dụng trong nhiều lĩnh vực, chẳng hạn như vật lý, kỹ thuật, địa lý, quân sự, v.v.
Giải bài toán về góc
- Công thức lượng giác sin cos cũng rất phổ biến trong việc giải các bài toán liên quan đến góc. Ví dụ, chúng ta có thể sử dụng các công thức lượng giác để tìm thêm thông tin về một góc, chẳng hạn như độ lớn, tọa độ điểm hoặc mối quan hệ với các góc khác.
- Nắm vững các công thức lượng giác sẽ giúp chúng ta giải quyết các bài toán về góc trong nhiều ngành.
4. Cách nhớ nhanh các công thức sin cos
Việc nhớ nhanh các công thức lượng giác sin cos là rất quan trọng để thuần thục và vận dụng hiệu quả chúng. Đây là một số gợi ý về cách tăng cường khả năng nhớ các công thức này:
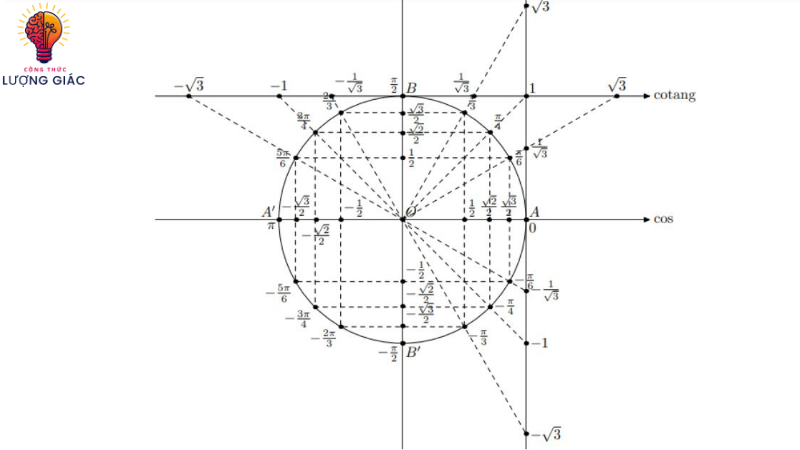
- Sử dụng ký niệm hình ảnh: Kết hợp các công thức với các ý tưởng hình ảnh là một cách hiệu quả để nhớ chúng. Ví dụ, để nhớ các giá trị cơ bản của sin và cos, chúng ta có thể liên tưởng hình ảnh đơn vị đường tròn và vị trí của các góc đặc biệt như 0, π/6, π/4, π/3 và π/2.
- Liên kết với tam giác vuông: Các công thức lượng giác được liên kết với các tam giác vuông cũng rất hữu ích. Ví dụ, bằng cách liên tưởng đến một tam giác vuông có cạnh kề a, cạnh đối b và cạnh huyền c, chúng ta có thể nhớ rằng sin(θ) = b/c và cos(θ) = a/c.
- Sử dụng mnemonic (phương pháp ghi nhớ): Các phương pháp ghi nhớ, còn được gọi là mnemonic, cũng là một phương pháp hiệu quả để nhớ các công thức lượng giác. Có thể liên kết nó với câu “Một số mèo ghét hành tây” để nhớ công thức sin2(x) + cos2(x) = 1. Nhớ các công thức lượng giác sin cos sẽ nhanh chóng và thuần thục hơn khi kết hợp các phương pháp trên.

5. Tính chất đối xứng của hàm sin và cos
Chúng ta phải hiểu các tính chất đối xứng của các hàm số này ngoài các ý nghĩa và ứng dụng của công thức lượng giác sin cos.
Tính chất đối xứng chẵn của hàm cos
Có thể nói rằng hàm số cos(x) có tính chất đối xứng chẵn, tức là:
- cos(-x) bằng cos(x).
- Điều này cho thấy rằng khi đối xứng qua trục y, giá trị của hàm cos không thay đổi. Nói cách khác, cos(x) và cos(-x) đều có giá trị tương tự.
Tính chất đối xứng lẻ của hàm sin
Trái ngược với điều này, hàm số sin(x) có tính chất đối xứng lẻ:
- sin(-x) và = -sin
- Tóm lại, giá trị của hàm sin sẽ thay đổi khi đối xứng với trục y. Ngoài ra, có thể hiểu được rằng sin(x) và sin(-x) là các giá trị đối nhau.
- Các tính chất đối xứng Điều này sẽ giúp nhận dạng và sử dụng các công thức định lượng một cách dễ dàng hơn.
6. Kết luận
Một trong những khái niệm cơ bản nhất trong toán học, công thức giác giác cos đã được giải quyết trong bài viết này . Chúng tôi đã xem xét ý nghĩa học tập của các công thức này và sự phổ biến của chúng trong nhiều lĩnh vực.
Tóm lại, công thức lượng giác sin và cos đóng vai trò quan trọng trong toán học và ứng dụng thực tế, giúp giải quyết nhiều bài toán hình học và vật lý. Việc nắm vững và vận dụng linh hoạt những công thức này sẽ giúp bạn tự tin hơn trong quá trình học tập và nghiên cứu. Hy vọng với những kiến thức trên, bạn có thể ứng dụng tốt trong mọi tình huống liên quan đến lượng giác.
Bệnh hen suyễn đôi khi cũng cần sự thấu hiểu và kiên trì như khi học công thức lượng giác vậy, chi tiết xin truy cập websitecongthucluonggiac.net xin cảm ơn!