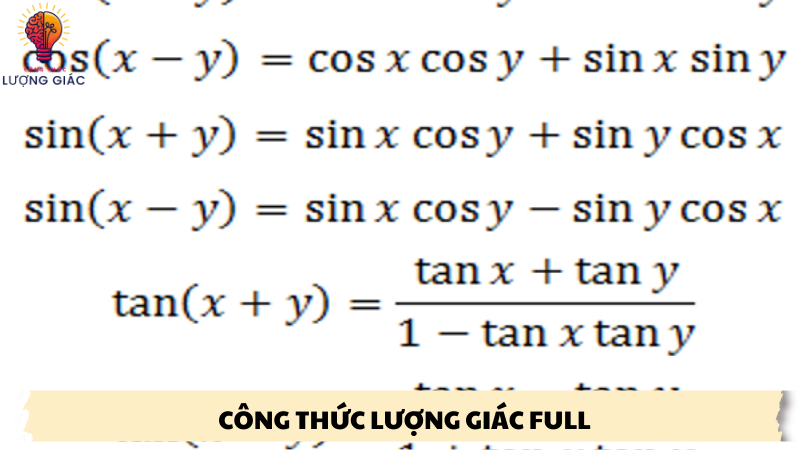Công thức lượng giác full từ những công thức đơn giản nhất đến những công thức phức tạp nhất , bài viết này sẽ cung cấp cho bạn cái nhìn toàn diện về các công thức lượng giác đầy đủ . Nó cũng cung cấp các lời khuyên để ghi nhớ kết quả .
1. Công thức lượng giác full
Công thức lượng giác full là nền tảng cho mọi công thức và ứng dụng phức tạp khác . Để có thể tự động giải quyết các bài toán giác độ , bạn phải hiểu rõ các công thức này. Chúng không chỉ là những ký hiệu và con số khô mà còn là mối liên hệ giữa đại số và hình học, giúp chúng ta hiểu rõ hơn về thế giới xung quanh .
Định nghĩa các hàm số lượng giác
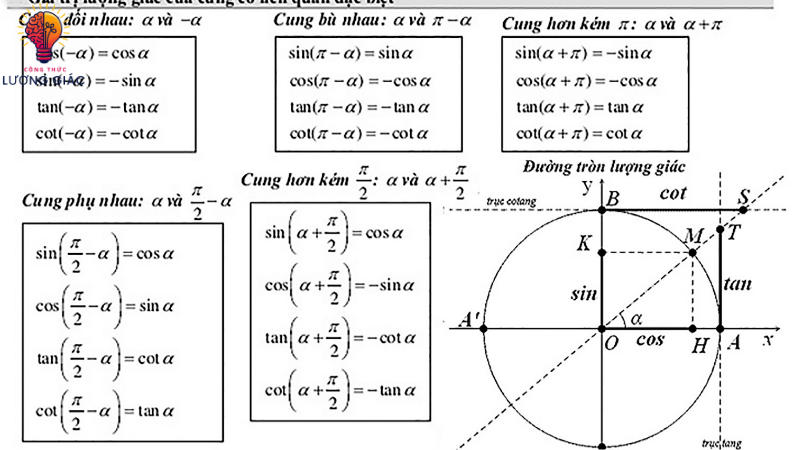
Công thức lượng giác full như sin, cos, tan và cot được định nghĩa bằng một đường tròn có bán kính bằng1. Một điểm trên đường tròn này tương ứng với một góc lượng giác, và dựa trên tọa độ của điểm đó, các giá trị của sin, cos, tan và cot được tìm thấy.
- Tung độ của điểm tương ứng trên đường tròn lượng giác là sin của một góc (thường được gọi là sin(α). Hoàn độ của điểm đó là cos của góc (cos(α))
- Tan của một góc (tan(α)) là tỉ số giữa sin và cos (tan(α) = sin(α)/cos(α))
- cot của một góc (cot(α)) là nghịch đảo của tan (cot(α) = cos(α)/sin(α).
- Điều thú vị ở đây là các giá trị sin, cos, tan và cot sẽ thay đổi theo một quy luật nhất định khi góc α thay đổi. Chúng không chỉ là những khái niệm trừu tượng mà còn thể hiện sự thay đổi và tuần hoàn trong toán học và nhiều hiện tượng tự nhiên.
2. Mối quan hệ cơ bản giữa các hàm số lượng giác
Công thức lượng giác full phụ thuộc vào nhau thay vì hoạt động một cách độc lập. Công thức Pythagoras trong lượng giác là một trong những mối quan hệ quan trọng nhất. Công thức này được thể hiện bằng sin2(α) + cos2(α) = 1.
Giá trị đặc biệt của các góc lượng giác
Công thức lượng giác full cụ thể như 0, 30, 45, 60 và 90 độ Các giá trị sin, cos, tan và cot là những giá trị quen thuộc và thường được sử dụng trong các bài toán. Bạn sẽ tránh được những sai sót không đáng có và tiết kiệm thời gian khi làm bài.
Chẳng hạn
- sin(0°) = 0, cos(0°) = 1;
- sin(30°) = 1/2, cos(30°) = √3/2
- sin(45°) = cos(45°) = √2/2; sin(60°) = √3/2
- cos(60°) = 1/2; sin(90°) = 1, cos(90°) = 0
Chúng ta không chỉ cần nắm bắt các giá trị này, mà chúng ta cũng cần hiểu tại sao chúng có giá trị. Điều này sẽ giúp chúng ta nhớ được nhiều hơn và dễ dàng suy luận khi cần thiết.
3. Ứng dụng của công thức lượng giác trong toán học
Công thức lượng giác full là một phần của giáo dục toán học phổ thông mà còn là một công cụ mạnh mẽ được sử dụng trong nhiều lĩnh vực toán học. Lượng giác đóng một vai trò quan trọng trong mọi lĩnh vực, từ giải phương trình và bất phương trình đến nghiên cứu các tính chất của hàm số. Tầm nhìn toán học của bạn sẽ được mở rộng khi bạn hiểu những ứng dụng này. Bạn cũng sẽ hiểu được giá trị của lượng giác.
Giải phương trình lượng giác
- Công thức lượng giác full trong đó các biểu thức lượng giác như sin, cos, tan và cot có ẩn số được gọi là phương trình lượng giác. Để giải quyết các phương trình này, chúng ta phải sử dụng các công thức lượng giác và các phép biến đổi tương tự.
- Không giống như phương trình đại số thông thường, các phương trình lượng giác cơ bản như sin(x) = a, cos(x) = b, tan(x) = c và cot(x) = d thường có vô số nghiệm.
Giải bất phương trình lượng giác
- Công thức lượng giác full cũng là một loại hoạt động phổ biến, giống như phương trình. Để giải quyết bất phương trình này, chúng ta cần kết hợp việc sử dụng các công thức lượng giác với việc kiểm tra dấu của các hàm số lượng giác trên đường tròn lượng giác.
- Lượng giác bất phương trình thường phức tạp hơn phương trình vì chúng ta cần tìm ra một khoảng giá trị hơn là một số giá trị nghiệm.
Nghiên cứu tính chất của hàm số lượng giác
- Công thức lượng giác full như sin(x), cos(x), tan(x) và cot(x) không chỉ là các công cụ giải toán mà còn là một chủ đề đáng chú ý để nghiên cứu. Chúng tôi quan tâm đến các tính chất của các hàm số này, chẳng hạn như tính chẵn lẻ, tính tuần hoàn, các khoảng đồng biến và nghịch biến cũng như các giá trị lớn nhất và nhỏ nhất.
4. Các công thức lượng giác cho tam giác vuông
Công thức lượng giác full đóng một vai trò quan trọng trong việc giải quyết các bài toán liên quan đến tam giác vuông, một trong những hình học cơ bản nhất. Nắm vững các công thức này sẽ giúp chúng ta giải quyết các bài toán hình học dễ dàng hơn và hiệu quả hơn. Đặc biệt, kiến thức này có thể được sử dụng trong các lĩnh vực thực tiễn như đo đạc, kỹ thuật và vật lý.
Định nghĩa các tỉ số lượng giác trong tam giác vuông
Công thức lượng giác full các tỉ số lượng giác được định nghĩa dựa trên cạnh đối, cạnh kề và cạnh huyền của tam giác.
- Sin của một góc được định nghĩa là tỉ số giữa cạnh đối và cạnh huyền (sin(α) = cạnh đối/cạnh huyền)
- cos của một góc là tỉ số giữa cạnh kề và cạnh huyền (cos(α) = cạnh kề/cạnh huyền)
- tan của một góc là tỉ số giữa cạnh đối và cạnh kề (tan(α) = cạnh đối/cạnh kề)
- cot của một góc là nghịch đảo của tan (cot(α) = cạnh kề/cạnh đối).
Các công thức liên quan đến tam giác vuông
- Ngoài các định nghĩa cơ bản, chúng ta cũng có các công thức khác liên quan đến tam giác vuông. Ví dụ, định lý Pythagoras nói rằng bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông (a2 + b2 = c2). Một công cụ mạnh mẽ để khám phá các tính chất của tam giác vuông là định lý này kết hợp với các tỉ số lượng giác.

5. Ứng dụng của lượng giác trong các bài toán thực tế
Công thức lượng giác full có nhiều ứng dụng thực tế, không chỉ trong các bài toán hình học trên giấy. Để đo đạc, ví dụ, chúng ta có thể sử dụng lượng giác để tính độ cao của một ngọn núi hoặc chiều rộng của một con sông mà không cần phải đo trực tiếp. Xây dựng sử dụng lượng giác để xác định góc nghiêng và độ dốc của các công trình.
Công thức cộng và hiệu trong lượng giác
- Một trong những bộ công thức lượng giác quan trọng nhất là công thức cộng và hiệu; chúng cho phép biểu diễn các hàm số lượng giác của tổng hoặc hiệu hai góc qua các hàm số lượng giác của từng góc.
- Việc nắm vững và sử dụng thành thạo những công thức này sẽ giúp chúng ta giải quyết các bài toán lượng giác một cách hiệu quả hơn và đơn giản hóa các biểu thức phức tạp.
Công thức cộng các góc lượng giác
Để tính sin, cos và tan của tổng hai góc, hãy sử dụng công thức cộng các góc lượng giác. Cụ thể, các công thức sau đây có thể được áp dụng:
- sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
- cos(a + b) = cos(a)cos(b) – sin(a)sin(b)
- tan(a + b) = (tan(a) + tan(b))/(1 – tan(a)tan(b)
Những công thức này không có tự nhiên; chúng được lấy từ các định nghĩa và mối quan hệ lượng giác cơ bản.
Công thức hiệu các góc lượng giác
Công thức hiệu, giống như công thức cộng, cho phép tính sin, cos và tan của hiệu hai góc. Cụ thể
- sin(a-b) = sin(a)cos(b) – cos(a)sin(b)
- cos(a-b) = cos(a)cos(b) + sin(a)sin(b)
- tan(a-b) = (tan(a) – tan(b))/(1 + tan(a)tan(b).
Công thức cộng và công thức hiệu có mối quan hệ chặt chẽ. Công thức hiệu có thể được tìm thấy bằng cách thay thế b trong công thức cộng bằng -b và sử dụng tính chất của sin và cos đối với góc âm.
Ứng dụng của công thức cộng và hiệu
- Trong việc giải các bài toán lượng giác, cả công thức cộng và hiệu đều rất phổ biến. Chúng có thể được sử dụng để giải quyết các phương trình lượng giác, biến đổi các biểu thức phức tạp hoặc tìm các giá trị của hàm số lượng giác ở các góc không quen thuộc.
6. Công thức nhân đôi và nửa góc trong lượng giác
Công thức lượng giác full là những công cụ hữu ích để biểu diễn các hàm số lượng giác của các góc liên quan đến các góc đã biết.
Công thức nhân đôi
Công thức nhân đôi cho phép ta tính sin, cos, tan của một góc gấp đôi góc đã biết.
Cụ thể công thức
- sin(2a) = 2sin(a)cos(a)
- cos(2a) = cos²(a) – sin²(a) = 2cos²(a) – 1 = 1 – 2sin²(a)
- tan(2a) = 2tan(a) / (1 – tan²(a)).
Các công thức này không tự nhiên mà có, chúng được suy ra từ các công thức cộng bằng cách thay b bằng a.
Công thức nửa góc
Công thức nửa góc cho phép ta tính các tỉ số lượng giác của một góc bằng một nửa góc đã biết. Cụ thể, các công thức này thường được viết dưới dạng:
- sin²(a/2) = (1 – cos(a)) / 2, cos²(a/2) = (1 + cos(a)) / 2
- tan(a/2) = sin(a) / (1 + cos(a)) = (1 – cos(a)) / sin(a).
- Các công thức này được suy ra từ công thức nhân đôi và công thức sin²(a)+cos²(a)=1 .
Mối quan hệ giữa công thức nhân đôi và nửa góc
- Công thức nửa góc và công thức nhân đôi rất liên quan với nhau . Nửa góc công thức về cơ bản là một biến thể của công thức nhân đôi.
- Ví dụ: ta có thể tìm ra công thức tính toán cos2(a/2) để từ cos(2a) = 2cos2(a) – 1. Hiểu được mối quan hệ này giúp chúng ta có cái nhìn sâu sắc hơn về lượng giác và chúng ta không cần phải học thuộc quá nhiều công thức bằng một cách máy móc.
7. Bảng công thức lượng giác đầy đủ
Công thức lượng giác full và tra cứu dễ dàng hơn , bảng tóm tắt các công thức giác độ đầy đủ đã đề cập trong bài viết được cung cấp dưới đây. Các công thức giác cơ bản , công thức cộng, trừ, nhân đôi , nửa góc và các biến đổithường được tìm thấy trong bảng này. Hy vọng bảng này sẽ là một người bạn đồng hành đáng tin cậy cho bạn trong quá trình học môn lượng giác.
| Công thức | Mô tả |
|---|---|
| Công thức cơ bản | |
| sin²(α) + cos²(α) = 1 | Quan hệ cơ bản giữa sin và cos |
| tan(α) = sin(α)/cos(α) | Định nghĩa tan |
| cot(α) = cos(α)/sin(α) | Định nghĩa cot |
| cot(α) = 1/tan(α) | Quan hệ giữa tan và cot |
| Công thức cộng | |
| sin(a + b) = sin(a)cos(b) + cos(a)sin(b) | Sin của tổng hai góc |
| cos(a + b) = cos(a)cos(b) – sin(a)sin(b) | Cos của tổng hai góc |
| tan(a + b) = (tan(a) + tan(b))/(1 – tan(a)tan(b)) | Tan của tổng hai góc |
| Công thức hiệu | |
| sin(a – b) = sin(a)cos(b) – cos(a)sin(b) | Sin của hiệu hai góc |
| cos(a – b) = cos(a)cos(b) + sin(a)sin(b) | Cos của hiệu hai góc |
| tan(a – b) = (tan(a) – tan(b))/(1 + tan(a)tan(b)) | Tan của hiệu hai góc |
| Công thức nhân đôi | |
| sin(2a) = 2sin(a)cos(a) | Sin của góc gấp đôi |
| cos(2a) = cos²(a) – sin²(a) | Cos của góc gấp đôi (dạng 1) |
| cos(2a) = 2cos²(a) – 1 | Cos của góc gấp đôi (dạng 2) |
| cos(2a) = 1 – 2sin²(a) | Cos của góc gấp đôi (dạng 3) |
| tan(2a) = 2tan(a)/(1 – tan²(a)) | Tan của góc gấp đôi |
| Công thức nửa góc | |
| sin²(a/2) = (1 – cos(a)) / 2 | Sin bình phương của góc một nửa |
| cos²(a/2) = (1 + cos(a)) / 2 | Cos bình phương của góc một nửa |
| tan(a/2) = sin(a) / (1 + cos(a)) | Tan của góc một nửa |
| tan(a/2) = (1 – cos(a)) / sin(a) | Tan của góc một nửa (dạng khác) |
| Biến đổi tích thành tổng | |
| sin(a)cos(b) = 1/2[sin(a+b) + sin(a-b)] | |
| cos(a)cos(b) = 1/2[cos(a+b)+cos(a-b)] | |
| sin(a)sin(b) = 1/2[cos(a-b) – cos(a+b)] | |
| Biến đổi tổng thành tích | |
| sin(a)+sin(b) = 2sin[(a+b)/2]cos[(a-b)/2] | |
| sin(a) – sin(b) = 2cos[(a+b)/2]sin[(a-b)/2] | |
| cos(a)+cos(b) = 2cos[(a+b)/2]cos[(a-b)/2] | |
| cos(a) – cos(b) = – 2sin[(a+b)/2]sin[(a-b)/2] |
8. Cách ghi nhớ công thức lượng giác hiệu quả
Ghi nhớ các công thức lượng giác full có thể là một thách thức đối với nhiều người. Tuy nhiên, đừng lo lắng, có rất nhiều cách để bạn có thể ghi nhớ chúng một cách hiệu quả mà không phải làm quá nhiều việc. Tìm ra phương pháp phù hợp nhất với bạn và kiên trì luyện tập là điều quan trọng. Hãy xem xét các chiến lược sau đây và chọn những chiến lược mà bạn thấy hữu ích nhất.
- Ghi nhớ bằng cách hiểu bản chất: Hiểu bản chất của các công thức lượng giác là một trong những cách hiệu quả nhất để ghi nhớ chúng. Hãy suy nghĩ về cách công thức được hình thành và mối liên hệ giữa chúng với đường tròn lượng giác, thay vì cố gắng học thuộc máy móc. Hiểu bản chất sẽ giúp bạn nhớ công thức một cách tự nhiên hơn.
- Ghi nhớ bằng hình ảnh và sơ đồ: Một phương pháp rất hiệu quả đối với những người học theo thị giác là sử dụng hình ảnh và sơ đồ. Ví dụ, bạn có thể vẽ sơ đồ đường tròn lượng giác và đánh dấu sin, cos, tan và cot. Bạn cũng có thể vẽ các tam giác vuông và ghi nhớ các tỉ số lượng giác của chúng. Màu sắc và hình ảnh sinh động sẽ giúp bạn nhớ và liên tưởng đến các công thức dễ dàng hơn.
- Ghi nhớ bằng cách luyện tập thường xuyên: Để ghi nhớ các công thức lượng giác, luyện tập thường xuyên là cách tốt nhất. Hãy thực hiện nhiều bài tập từ cơ bản đến phức tạp và cố gắng vận dụng các công thức một cách linh hoạt. Bài tập không chỉ giúp bạn nhớ công thức mà còn giúp bạn hiểu cách áp dụng chúng vào cuộc sống thực tế.
9. Kết luận
Chúng tôi đã xem xét chi tiết các công thức giác giác đầy đủ trong bài viết này, từ các công thức cơ bản của các công thức phức tạp, cũng như nhiều ứng dụng và cách ghi nhớ hiệu quả. Lượng giác không chỉ là một chủ đề khô khan mà còn là một phương tiện mạnh mẽ để mở ra những cửa sổ toán học kỳ diệu.
Các công thức lượng giác không chỉ giúp giải quyết nhiều bài toán hình học mà còn là công cụ quan trọng trong các lĩnh vực như kỹ thuật, vật lý và đời sống hàng ngày. Việc nắm vững và vận dụng linh hoạt những công thức này giúp chúng ta tự tin giải quyết các vấn đề từ cơ bản đến nâng cao. Tuy nhiên, để học hiệu quả, bạn cần thường xuyên luyện tập và áp dụng vào thực tế.
Bên cạnh việc học tập, chúng ta cũng cần quan tâm đến sức khỏe và phòng tránh các dịch bệnh mới nổi, chẳng hạn như bệnh đậu mùa khỉ,chi tiết xin truy cập websitecongthucluonggiac.net xin cảm ơn!