Công thức lượng giác trong tam giác là một phần quan trọng của toán học, đặc biệt là hình học. Việc nắm vững công thức này không chỉ giúp học sinh làm bài tập hiệu quả hơn mà còn giúp họ suy nghĩ sáng tạo để giải quyết các vấn đề thực tế. Trong bài viết này, bạn sẽ nhận được sự hiểu biết sâu sắc về các công thức lượng giác trong tam giác và các ứng dụng của chúng. Bạn cũng sẽ tìm hiểu cách sử dụng chúng để tính diện tích của một tam giác và xác định mối quan hệ giữa các cạnh và góc Tìm hiểu thế giới thú vị của lượng giác với tôi!
1. Công thức lượng giác trong tam giác cơ bản
Tam giác lượng giác bao gồm các công thức cơ bản và nhiều ứng dụng khác nhau. Bạn sẽ trở nên tự tin hơn khi giải quyết các bài toán liên quan nếu bạn hiểu những công thức này.
Định nghĩa và ý tưởng cơ bản
- Trước hết, chúng ta phải hiểu khái niệm cơ bản của công thức lượng giác và định nghĩa của nó. Các công thức lượng giác cho thấy mối quan hệ giữa các cạnh và góc trong bất kỳ tam giác nào.
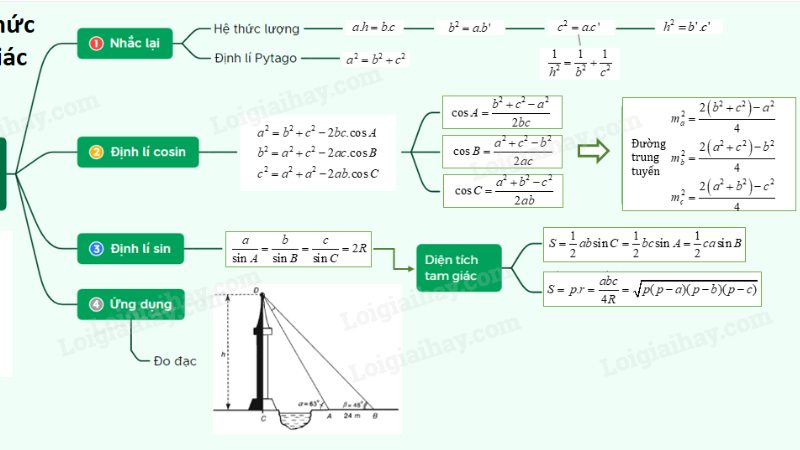
Công thức lượng giác cơ bản bao gồm cụ thể:
Định lý Tangent, Định lý Sin và Định lý Cosin
- Mỗi công thức đều hữu ích trong các tình huống nhất định. Nắm vững khái niệm và định nghĩa này sẽ là bước đầu tiên quan trọng trong việc nghiên cứu sâu hơn về lượng giác.
- Theo định lý sin, tỉ lệ giữa độ dài của một cạnh đối diện với một góc trong một tam giác và sin của góc đó là hằng số. Trong một trường hợp cụ thể, nếu ABC là một tam giác với các cạnh a, b và c tương ứng đối diện với các góc A, B và C, thì: [a sin A} = b sin B = c sin C]
- Khi bạn biết hai góc và một cạnh (AAS hoặc ASA) hoặc hai góc và một góc không kề (SSA), Định lý Sin rất hữu ích.
- Định lý Cosin, trong khi đó, được sử dụng để xác định chiều dài của một cạnh khi bạn biết hai cạnh còn lại cũng như góc kề bên của chúng. [c^2 = a^2 + b^2 – 2ab ⋅ cos C] là công thức.
- Định lý này cho phép tính toán dễ dàng chiều dài của một cạnh trong một tam giác mà không cần tìm ra các góc của nó.
Định lý của tầng
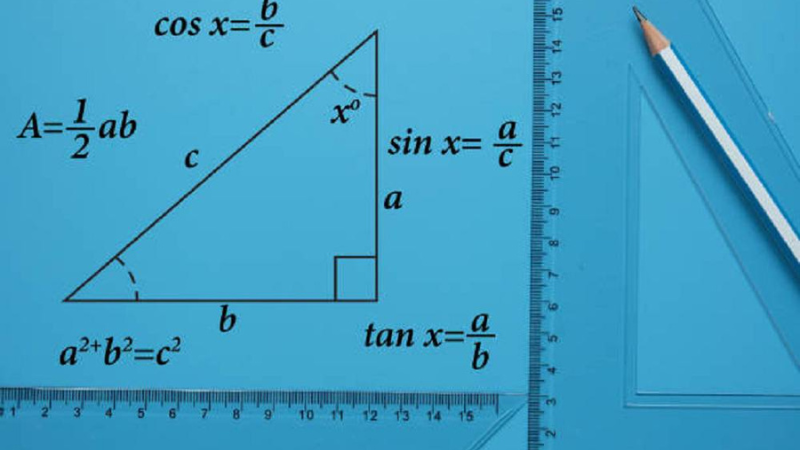
- Cuối cùng, tam giác vuông sử dụng rất nhiều Định lý Tangent. Theo định lý này, [tan A = frac{h}{d} ]
- Trong đó, chiều cao từ đỉnh A xuống đáy d được gọi là h. Điều này rất hữu ích khi tính toán diện tích và chiều cao của tam giác vuông.
2. Ứng dụng công thức lượng giác trong tam giác để giải toán
Bước tiếp theo là khám phá cách áp dụng các công thức cơ bản để giải các bài toán tam giác. Những ứng dụng này không chỉ giúp giải quyết bài tập mà còn cải thiện kiến thức của bạn.
- Giải tam giác không vuông với Định lý Sin Nếu bạn biết một cạnh và hai góc, việc tìm ra các góc còn lại trở nên đơn giản hơn bao giờ hết.
- Xem xét tam giác ABC với góc A là 30 độ, góc B là 60 độ và cạnh a là 10. Cạnh b và c có thể được tìm thấy bằng cách sử dụng Định lý Sin.
- Điều này không chỉ giúp bạn hoàn thành bài tập mà còn giúp bạn suy nghĩ logic và giải quyết vấn đề.
- Giải tam giác bằng Định lý Cosin: Định lý Cosin là phương pháp tuyệt vời để giải quyết một tam giác có hai cạnh và một góc kề bên. Bạn có thể nhanh chóng xác định chiều dài của cạnh còn lại bằng cách sử dụng công thức.
- Định lý Cosin sẽ giúp bạn tăng độ chính xác và tiết kiệm thời gian, đặc biệt trong các bài toán trắc nghiệm.
3. Cách sử dụng công thức lượng giác trong tam giác để tính diện tích tam giác
Có nhiều công thức để tính toán diện tích của một tam giác vì đây là dữ liệu quan trọng. Tùy thuộc vào nguồn lực của bạn, mỗi công thức có ưu điểm và ứng dụng riêng.
Công thức để xác định diện tích tam giác từ chiều cao và cạnh
- Công thức được sử dụng phổ biến nhất để xác định diện tích của một tam giác là [S = frac{1}{2} ⋅ a ⋅ h], trong đó a là chiều dài của cạnh đáy và h là chiều cao từ đỉnh xuống cạnh đáy. Phương pháp này trực quan và dễ hiểu, nhưng chỉ nên sử dụng nếu bạn có chiều cao.
Công thức tính diện tích sử dụng định lý Sin
- Ngoài ra, để tính diện tích của một tam giác, bạn có thể sử dụng Định lý Sin. S = frac{1{2} a b sin C là công thức.
- Trong đó, C là góc giữa hai cạnh và a và b là chiều dài của chúng.
Theo công thức của Heron
- Cuối cùng, bạn có thể sử dụng công thức Heron để tìm diện tích của tam giác nếu bạn biết tất cả ba cạnh của nó. Công thức được đưa ra như sau:
- [S = sqrt{s(s-a)(s-b)(s-c)}]
- Trong trường hợp này, s là nửa chu vi của tam giác, được tìm thấy bằng công thức sau: [s = \frac{a+b+c}{2}]
- Công thức này rất mạnh vì nó có thể tính diện tích của tam giác mà không cần biết góc.
4. Ví dụ minh họa về công thức lượng giác trong tam giác
Để hiểu rõ hơn về cách áp dụng các công thức lượng giác trong tam giác, hãy tham khảo cùng một điểm.
- Ví dụ, giả sử bạn có một tam giác ABC với góc A=45°, góc B=60° và cạnh a=10. Các cạnh b và c có thể được tìm thấy bằng cách sử dụng định lý Sin, điều này dễ dàng cho việc tính diện tích.
Một ví dụ về việc sử dụng định lý Cosin
- Tam giác DEF có các cạnh d=8, e=6 và góc F=60°. Định lý Cosin có thể được sử dụng để tính chiều dài của cạnh f.
Chẳng hạn, tính diện tích
- Bạn có thể nhanh chóng tính toán diện tích của một tam giác GHI với cạnh g=5, h=7 và góc I=30 độ bằng công thức diện tích của Định lý Sin.

5. Lợi ích của việc nắm vững công thức lượng giác trong tam giác
Nắm vững công thức lượng giác trong tam giác không chỉ giúp bạn học tập mà còn mang lại nhiều lợi ích khác trong cuộc sống hàng ngày và công việc.
- Giúp nâng cao khả năng suy nghĩ: Lượng giác không chỉ là một ngành học mà còn là một phương pháp suy nghĩ. Phát triển khả năng tư duy logic và phân tích của bạn sẽ được hưởng lợi từ việc giải quyết các bài toán lượng giác.
- Ứng dụng thực hành: Lượng giác rất quan trọng trong nhiều lĩnh vực, từ kiến trúc đến kỹ thuật. Bạn sẽ dễ dàng áp dụng các công thức này.
- Tăng sự tự tin: Cuối cùng, nắm vững công thức lượng giác sẽ khiến bạn cảm thấy tự tin hơn khi học tập và làm việc. Giải quyết các bài toán khó khăn sẽ dễ dàng hơn khi bạn tin tưởng vào kiến thức của mình.
- Giải quyết các bài toán liên quan đến lượng giác và hình học: Nắm vững các công thức lượng giác giúp bạn dễ dàng giải quyết các bài toán liên quan đến tam giác, tìm cạnh, góc hoặc diện tích của một tam giác một cách nhanh chóng và chính xác.
- Cơ sở cho nâng cao: Nhiều lĩnh vực nâng cao như giải tích, đại số tuyến tính, toán học ứng dụng và khoa học máy tính phụ thuộc vào lượng giác. Bạn sẽ học được các môn học phức tạp hơn nếu bạn sử dụng các công thức này.
- Mở rộng khả năng giải quyết vấn đề công việc: Công thức lượng giác trong tam giác được sử dụng trong các lĩnh vực như kỹ thuật, kiến trúc, nhà thiết kế và lập trình viên để tối ưu hóa công việc và giải quyết các vấn đề liên quan đến tính toán và thiết kế.
Hiểu và sử dụng thành thạo các công thức lượng giác trong tam giác có nhiều ứng dụng thiết thực trong cuộc sống và sự nghiệp, ngoài việc giúp bạn học tốt hơn về toán học.
6. Kết quả
Trong toán học, công thức lượng giác trong tam giác là một phần quan trọng. Việc sử dụng các công thức này không chỉ giúp bạn hoàn thành bài tập hiệu quả mà còn giúp bạn suy nghĩ và áp dụng chúng trong cuộc sống thực tế. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về công thức lượng giác của tam giác. Để trở thành một người thành thạo trong lĩnh vực này. Ngoài ra một vấn đề rất quan trọng cần được chú ý, đó là bệnh giang mai rất nguy hiểm.
Trên đây là bài viết công thức lượng giác trong tam giác , chi tiết xin truy cập website: congthucluonggiac.net xin cảm ơn!
