6 công thức lượng giác cơ bản là những công thức toán học cơ bản giúp chúng ta hiểu và giải quyết các bài toán và khái niệm liên quan đến tam giác vuông. Những công thức này không chỉ quan trọng trong toán học mà còn được sử dụng rộng rãi trong kỹ thuật, vật lý và thậm chí cả cuộc sống hàng ngày.
1. Giới thiệu về 6 công thức lượng giác cơ bản
Khái niệm về lượng giác
- Toán học lượng giác xem xét các mối quan hệ giữa các góc và cạnh của một tam giác vuông. Sin, cos, tan, cot, sec và csc là những khái niệm cơ bản về lượng giác. Chúng tôi sử dụng các khái niệm này để mô tả các đặc tính hình học của tam giác vuông.
6 công thức lượng giác cơ bản
Các công thức lượng giác thông thường bao gồm:
- sin(x) = đối/huyền
- cos(x) = kề/huyền
- tan(x) = đối/kề
- cot(x) = kề/đối
- sec(x) = huyền/kề
- csc(x) = huyền/đối
Các công thức này giúp tính toán và giải các bài toán lượng giác bằng cách minh họa mối quan hệ giữa các cạnh và góc trong tam giác vuông.
Ý nghĩa của 6 công thức lượng giác cơ bản
- Những công thức lượng giác cơ bản có ý nghĩa hình học và không chỉ là các phép tính toán. Bằng cách sử dụng chúng trong việc giải quyết các bài toán lượng giác, chúng tăng cường sự hiểu biết về mối quan hệ giữa các cạnh và góc của một tam giác vuông.
- Để vận dụng tam giác vuông hiệu quả hơn trong các bài toán thực tế, chúng ta cần nắm bắt sáu công thức này.
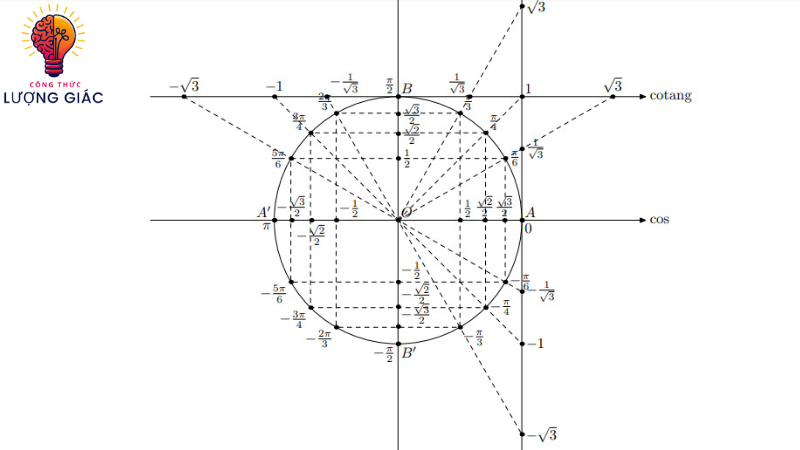
2. Ý nghĩa của 6 công thức lượng giác cơ bản trong toán học
Vai trò trong tam giác vuông
- Việc mô tả và tính toán các đặc tính của tam giác vuông phụ thuộc vào các công thức lượng giác cơ bản. Chúng hỗ trợ xác định các cạnh và góc của tam giác vuông dựa trên các mối quan hệ toán học.
- Ví dụ, nếu biết một cạnh và một góc của một tam giác vuông, chúng ta có thể sử dụng các công thức lượng giác cơ bản để tính toán các cạnh và góc còn lại của tam giác.
Ứng dụng trong giải toán
- Khi giải các bài toán lượng giác, các công thức lượng giác cơ bản là một công cụ không thể thiếu. Các yếu tố của tam giác vuông có thể được tính toán nhanh chóng và chính xác với sự hỗ trợ của chúng, điều này giúp chúng ta đạt được kết quả cuối cùng.
- Ngoài ra, các công thức này được sử dụng rộng rãi trong các bài toán trong các lĩnh vực hình học, vật lý và kỹ thuật. Để giải quyết các bài toán hiệu quả hơn, chúng ta nên học sáu công thức lượng giác cơ bản.
Mối liên hệ với các khái niệm toán học khác
- Các công thức lượng giác cơ bản không chỉ rất quan trọng trong lĩnh vực lượng giác mà còn liên quan đến nhiều khái niệm toán học khác, chẳng hạn như hàm số, tam giác, giá trị lớn nhất hoặc nhỏ nhất, v.v.
- Hiểu được các mối liên hệ này sẽ giúp chúng ta tiếp cận và vận dụng các công thức lượng giác cơ bản hơn. Điều này sẽ giúp chúng ta giải quyết các bài toán toán học phức tạp hơn.
3. Cách ghi nhớ 6 công thức lượng giác cơ bản
Phương pháp mnemonic
- Phương pháp ghi nhớ mnemonic là một phương pháp hiệu quả để ghi nhớ sáu công thức lượng giác cơ bản. Chúng tôi có thể liên kết các công thức với hình ảnh, từ hoặc câu dễ nhớ bằng cách sử dụng phương pháp này.
- Chúng ta có thể sử dụng câu “Sọ Cô Có Tác Dụng Sống” (Sin, Cos, Cot, Tan, Csc, Sec) để nhớ sáu công thức.
Liên hệ với tam giác vuông
- Liên kết 6 công thức lượng giác cơ bản với hình ảnh tam giác vuông là một cách khác để ghi nhớ chúng. Bằng cách này, chúng ta có thể dễ dàng nhớ được cách các cạnh và góc liên kết với nhau, điều này cho phép chúng ta áp dụng công thức phù hợp cho từng trường hợp.
- Ví dụ, chúng ta có thể hình dung tam giác vuông, nhớ rằng sin(x) là tỉ số giữa cạnh đối và cạnh huyền, cos(x) là tỉ số giữa cạnh kề và cạnh huyền, v.v.
Luyện tập và áp dụng thực tế
- Ngoài việc sử dụng các phương pháp để ghi nhớ, cũng rất quan trọng là học cách áp dụng các công thức lượng giác cơ bản vào các bài toán thực tế. Càng tập luyện nhiều, chúng ta càng thuần thục và nắm vững các công thức này.
- Trong khi giải quyết các bài toán, hãy cố gắng áp dụng các công thức một cách linh hoạt hơn là chỉ nhớ chúng. Điều này sẽ giúp chúng ta hiểu rõ hơn về ý nghĩa của mỗi công thức và cách chúng được sử dụng.
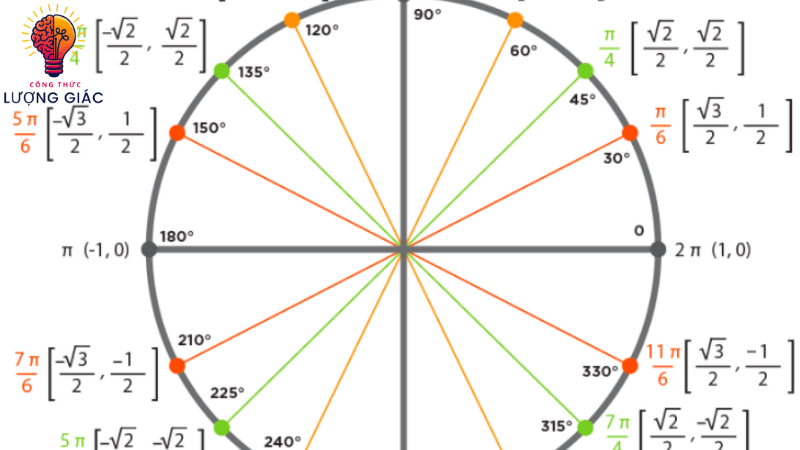
4. Ứng dụng của 6 công thức lượng giác cơ bản trong giải toán
Tính toán các yếu tố của tam giác vuông
- Như đã đề cập trước đây, 6 công thức lượng giác cơ bảnlà một công cụ quan trọng để giải quyết các bài toán liên quan đến tam giác vuông. Chúng hỗ trợ tính toán nhanh chóng và chính xác các cạnh và góc của tam giác vuông dựa trên các mối quan hệ toán học.
- Ví dụ, nếu chúng ta biết một cạnh và một góc của một tam giác vuông, chúng ta có thể sử dụng các công thức lượng giác cơ bản để tính toán các cạnh và góc còn lại của tam giác vuông.
Giải quyết các bài toán thực tế
- Các công thức lượng giác cơ bản được sử dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật, ngoài toán học. Chúng có thể được sử dụng để giải quyết các bài toán thực tế liên quan đến các yếu tố như độ cao, khoảng cách và góc nghiêng.
- Ví dụ, trong lĩnh vực xây dựng, các công thức lượng giác cơ bản sẽ được sử dụng để tính toán các góc nghiêng, độ dốc của mái nhà và độ cao của một tòa nhà. Các công thức này cũng được sử dụng để xác định vị trí, hướng di chuyển và khoảng cách.
Mô hình hóa và mô phỏng
- Trong các lĩnh vực khoa học và kỹ thuật, 6 công thức lượng giác cơ bản cũng được sử dụng để mô hình hóa và mô phỏng các hệ thống và quá trình. Để dự đoán và mô phỏng các hiện tượng một cách tin cậy, chúng giúp chúng ta tạo ra các mô hình toán học chính xác.
- Ví dụ, các công thức lượng giác cơ bản được sử dụng để xác định các góc tới, góc phản xạ và góc khúc xạ của sóng khi mô phỏng quá trình lan truyền sóng điện từ. Chúng ta cũng sử dụng các công thức này để xác định vị trí, vận tốc và gia tốc khi mô hình hóa chuyển động của các vật thể..
5. So sánh 6 công thức lượng giác cơ bản với các công thức khác
Công thức lượng giác nâng cao
- Các công thức lượng giác nâng cao như sin(2x), cos(2x), tan(2x) v.v. có sẵn ngoài sáu công thức lượng giác cơ bản. Các mối quan hệ giữa các cạnh và góc của một tam giác vuông được mô tả chi tiết hơn trong các công thức này.
- Việc nắm vững sáu công thức lượng giác cơ bản vẫn rất quan trọng, mặc dù các công thức nâng cao cung cấp thông tin chi tiết hơn. Trước khi tiếp cận các công thức nâng cao, chúng ta phải hiểu những công thức cơ bản.
Công thức trigonometric hợp
- Các công thức trigonometric hợp, chẳng hạn như sin(x) + cos(x), sin(x) – cos(x), v.v., có sẵn ngoài các công thức lượng giác cơ bản. Những công thức này cho thấy các mối quan hệ giữa nhiều hàm lượng giác.
- Các biểu thức lượng giác phức tạp hơn có thể được đơn giản hóa bằng cách sử dụng các công thức trigonometric hợp. Nhưng việc hiểu và sử dụng các công thức trigonometric hợp một cách hiệu quả cần phải hiểu sáu công thức lượng giác cơ bản.
Công thức lượng giác ngược
- Ngoài các công thức lượng giác cơ bản, chúng ta cũng cần nắm rõ các công thức lượng giác ngược, chẳng hạn như arcsin(x), arccos(x), arctan(x) và các công thức khác. Tính toán các góc dựa trên các giá trị của các hàm lượng giác được cung cấp bởi những công thức này.
- Khi chúng ta cần tìm ra các góc dựa trên các giá trị của các cạnh hoặc tỉ số lượng giác, các công thức lượng giác ngược thường được sử dụng. Sẽ hiệu quả hơn khi giải quyết các bài toán lượng giác nếu chúng ta biết mối quan hệ giữa các công thức lượng giác cơ bản và công thức lượng giác ngược.
6. Ví dụ minh họa cho 6 công thức lượng giác cơ bản
Ví dụ 1: Tính độ dài cạnh đối của tam giác vuông
Giả sử rằng chúng ta có một tam giác vuông ABC, trong đó:
- A = 30 độ
- Cạnh kề (AB) bằng sáu đơn vị.
- Tính độ dài cạnh đối (AC).
- Chúng ta sử dụng công thức lượng giác cơ bản để tính độ dài của cạnh đối: Đối/huyền = sin(x).
- Trong trường hợp góc A = 30 độ, sin(30°) = đối/huyền đối = sin(30°). = × huyền đối 1/2 × 6 tạo thành ba đơn vị.
Ví dụ 2: Tính độ dài cạnh kề của tam giác vuông
- Giả sử rằng chúng ta có một tam giác vuông PQR, trong đó:
- P = 60 độ
- Cạnh trung bình (QR) = 8 đ
Tính độ dài cạnh kề của tam giác vuông
Giả sử rằng chúng ta có một tam giác vuông PQR, trong đó:
- P = 60 độ
- Cạnh đối (QR) gồm tám đơn vị.
- Chúng ta sẽ sử dụng công thức lượng giác cơ bản để tính độ dài của cạnh kề (PQ): cos(x) = kề/huyền.
- Chúng ta có: cos(60°) = kề/huyền khi P = 60 độ. Nhưng trước tiên, chúng ta phải tìm độ dài huyền (PR) bằng cách sử dụng công thức sin: sin(60°) = đối/huyền.
- Do đó, huyền = đối/sin(60) = 8/sin(60).
- Khi biết rằng sin(60°) = √3/2, chúng ta có thể tìm thấy: huyền = 8/(√3/2) = 16/√3 = 16√3/3.
- Tiếp theo, chúng tôi tìm cạnh kề bằng cách sử dụng công thức cos: cos(60°) = kề/(16√3/3). Ngoài ra, kề = cos(60°) (1/2) × (16√3/3) = 8√3/3.
- Theo kết quả, cạnh kề PQ là 8√3/3 đơn vị. Ví dụ này cho thấy rõ ràng rằng việc sử dụng các công thức lượng giác không chỉ giúp giải quyết bài toán mà còn cho chúng ta thấy những mối quan hệ thú vị giữa các yếu tố trong tam giác vuông.
Ví dụ 3: Tính góc từ các cạnh đã biết
Giả sử chúng tôi có một tam giác vuông DEF, với:
- Cạnh kề (DE) có giá trị là năm đơn vị.
- Cạnh đối (EF) = mười hai đơn vị
- Chúng tôi muốn xác định giá trị của góc D. Để thực hiện điều này, chúng ta sẽ sử dụng hàm tang, theo công thức: tan(D) = đối/kề.
- Điều này cho thấy tan(D) = EF/DE = 12/5.
- Chúng ta sẽ sử dụng công thức lượng giác ngược để tìm góc D: D = arctan(12/5).
- Chúng ta có thể tính ra góc D khoảng 67.38 độ bằng máy tính hoặc bảng tra. Điều này chứng minh rằng các công thức lượng giác căn bản cho phép tính toán cạnh và góc của tam giác vuông dễ dàng.
7. Kết luận
Chúng ta có thể thấy từ nội dung đã đề cập rằng sáu công thức lượng giác cơ bản là nền tảng vững chắc cho việc hiểu và vận dụng cả hình học và lượng giác. Những công thức này không chỉ là lý thuyết mà còn được sử dụng trong nhiều lĩnh vực khác nhau, từ tính toán trong kỹ thuật xây dựng đến ứng dụng trong nghiên cứu khoa học.
Hiểu và nắm rõ các công thức này sẽ giúp bạn giải quyết các bài toán học thuật và áp dụng chúng vào cuộc sống hàng ngày. Hãy luôn nhớ rằng hiểu biết về các công thức lượng giác không chỉ là một phần của giáo dục mà còn là một công cụ mạnh mẽ để cải thiện khả năng giải quyết vấn đề và tư duy logic.
Trong khi đó, cũng như các kiến thức khác, việc hiểu và kiểm soát sức khỏe, đặc biệt là các bệnh tiểu đường, cũng đòi hỏi sự chăm sóc và hiểu biết cẩn thận để đạt được sự cân bằng và sức khỏe lâu dài, chi tiết xin truy cập website congthucluonggiac.net xin cảm ơn!

