Các công thức lượng giác cần nhớ có nhiều ứng dụng và rất quan trọng trong toán học. Khi nói đến các công thức lượng giác, bạn phải nhớ rằng chúng không chỉ là các phép toán mà còn là các nguyên lý và quy luật có thể giúp bạn giải quyết nhiều bài toán phức tạp hơn. Các công thức lượng giác cơ bản, đặc biệt là các mối quan hệ giữa các hàm lượng giác trong không gian hình học, sẽ được giải quyết trong bài viết này.
1. Các công thức lượng giác cần nhớ
Các công thức lượng giác cần nhớ phải được hiểu để bắt đầu. Các công thức phức tạp hơn có thể được xây dựng và áp dụng trên nền tảng này. Việc ghi nhớ và vận dụng các công thức lượng giác khác sẽ trở nên khó khăn nếu không nắm vững những công thức này.
Sine, Cosine và Tangent
Các công thức lượng giác cần nhớ nhất là sine, cosine và tangent, tất cả đều dựa trên một tam giác vuông.
- Sin của một góc là tỉ số giữa cạnh đối diện và cạnh huyền.
- Hàm cosine, còn được gọi là cos, là tỉ số giữa cạnh huyền và cạnh kề.
- Hàm tangent (tan), còn được gọi là hàm sine và cosine, hoặc tỉ số giữa cạnh đối diện và cạnh kề.
- Hãy nhớ các nguyên tắc chính: Các hàm lượng giác có nhiều giá trị riêng biệt mà chúng ta cần lưu ý. Chẳng hạn như:
- Trong thực tế, sin(0) = 0 và sin(30) = 1/2 sin(45) = √2/2 sin(60) = √3/2 sin(90) = 1. Những công thức và giá trị này không chỉ có trong sách giáo khoa mà còn được sử dụng trong nhiều lĩnh vực khác nhau, chẳng hạn như phân tích dữ liệu trong nghiên cứu khoa học và thiết kế cầu đường.
Công thức Pythagore
- Các công thức lượng giác cần nhớ, một trong những công thức lượng giác nổi tiếng nhất, cho phép xác định mối quan hệ giữa các cạnh của một tam giác vuông. Theo công thức, [a^2 + b^2 = c^2] trong đó cạnh huyền (c) và hai cạnh còn lại (a) và (b).
- Một số công thức lượng giác sử dụng công thức này để tính chiều dài cạnh của một tam giác. Các hàm lượng giác có thể được lấy từ đó.
Các công thức lượng giác khác
- cotangent
- Secant
- Có sẵn (csc)
- Nắm vững các công thức này sẽ nâng cao kiến thức của bạn và khả năng giải quyết vấn đề toán học của bạn.

2. Các công thức lượng giác đặc biệt
Chúng ta sẽ học các công thức lượng giác đặc biệt sau khi nắm vững các công thức lượng giác cần nhớ. Các bài toán phức tạp hơn và thường xuyên xuất hiện trong kỳ thi trở nên dễ dàng hơn nhờ các công thức này.
Các công thức cho các góc đặc biệt
- Ghi nhớ các giá trị của các hàm lượng giác ở các góc khác nhau là một yếu tố quan trọng trong lượng giác.
- Bạn nên chú ý đến các góc 0 độ, 30 độ, 45 độ, 60 độ và 90 độ.
- Sau đây là một ví dụ: cos(0) = 1 sin(30) = 1/2 tan(45) = 1
- Bạn sẽ tiết kiệm thời gian khi làm bài tập và kiểm tra bằng cách ghi nhớ các nguyên tắc này.
Các công thức cộng góc
- Các công thức lượng giác cần nhớ, các công thức cộng góc là một phần quan trọng. Chúng cho phép tính hàm lượng giác khi có tổng của hai góc.
- Chẳng hạn, sin(a + b) = sin(a) cos(b) + cos(a) sin(b) = cos(a) cos(b) – sin(a) sin(b).
Các công thức hiệu góc
- Một số công thức hiệu tiêu có thể được tìm thấy là:
- Sin(a – b) tương đương với sin(a) cos(b) và cos(a) sin(b).
- Cos(a – b) tương đương với cos(a) cos(b) và sin(a) sin(b).
- Ngoài ra, các công thức này giúp giải quyết các bài toán phức tạp nhanh chóng mà không cần sử dụng bảng lượng giác.
3. Công thức cộng và hiệu trong lượng giác
Các công thức lượng giác cần nhớ trong lượng giác rất quan trọng vì chúng cung cấp nền tảng cho việc tính toán các giá trị của các hàm lượng giác. Bạn sẽ có thể giải quyết nhiều bài toán khó khăn hơn nếu bạn hiểu và vận dụng những công thức này một cách linh hoạt.
Ý nghĩa của các công thức cộng
- Các công thức lượng giác cần nhớ trực tiếp các giá trị hàm lượng giác của hai góc mà không cần tìm giá trị cho từng góc. Điều này rất hữu ích cho những công việc yêu cầu tính toán nhanh chóng.
- Ví dụ, nếu bạn biết giá trị của sin(30°) và cos(60°), bạn có thể tìm dược sin(90°) bằng cách sử dụng công thức cộng. Việc này không chỉ tiết kiệm thời gian mà còn giảm sai sót trong tính toán.
Ý nghĩa của các công thức hiệu
- Các công thức lượng giác cần nhớ, công thức hiệu cũng cho phép xác định các giá trị hàm lượng giác bằng cách sử dụng một phương pháp trừ đi một phương pháp khác. Người học có thể dễ dàng áp dụng công thức vào các bài toán nhất định vì điều này.
- Chẳng hạn, bạn có thể sử dụng công thức hiệu với hai góc 45° và 30° để tìm sin(15°) mà không có giá trị này trong bảng lượng giác.
Ứng dụng trong các bài toán thực tiễn
- Các công thức lượng giác cần nhớ và hiệu được sử dụng thực tế trong nhiều lĩnh vực, chẳng hạn như vật lý, kỹ thuật và thậm chí cả kinh tế. Nó không chỉ làm cho việc tính toán trở nên dễ dàng hơn mà còn cung cấp những hiểu biết mới về cách các yếu tố trong một mô hình tương tác với nhau.
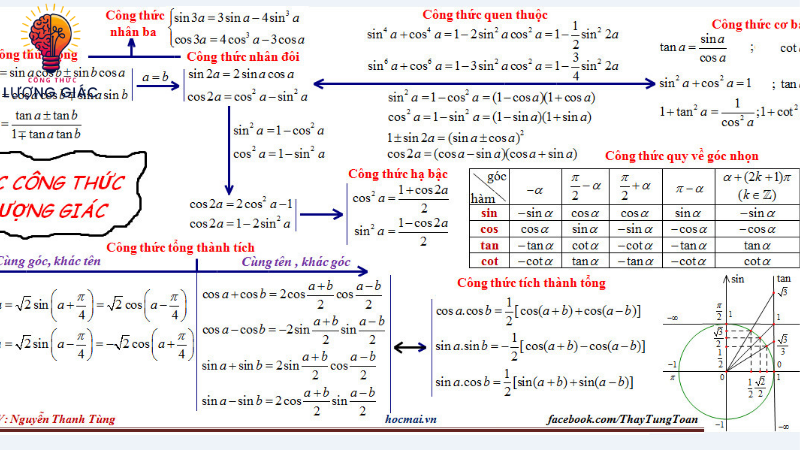
4. Công thức nhân đôi trong lượng giác
Các công thức lượng giác cần nhớ, công thức nhân đôi rất quan trọng vì nó hỗ trợ chuyển đổi giữa các góc và hàm lượng giác. Trong việc giải quyết các bài toán lượng giác phức tạp, những công thức này mang lại sự linh hoạt.
Công thức nhân đôi cho sine
- Các công thức lượng giác cần nhớ giá trị của hàm sine ở một góc gấp đôi có thể được tính toán bằng cách sử dụng công thức nhân đôi cho sine.
- Cụ thể, công thức được tìm thấy là [sin(2theta) = 2 sin(theta) và cos(theta)].
- Điều này có nghĩa là bạn có thể dễ dàng tìm ra sin(2θ) nếu bạn biết giá trị của sin(θ) và cos(θ).
Công thức nhân đôi cho cosine
- Tương tự như vậy, công thức nhân đôi cho cosine rất quan trọng: [cos(2theta) = cos^2(theta) – sin^2(theta) ]
- Ngoài ra, công thức này có thể được trình bày theo cách khác: [cos(2theta) = 2cos^2(theta) – 1] hoặc [cos(2theta) = 1 – 2sin^2(theta) ].
Ứng dụng thực tiễn
- Trong các bài toán quỹ đạo, dao động và nhiều ứng dụng vật lý khác, hàm nhân đôi rất hữu ích. Để đạt được hiệu quả cao nhất, người học không chỉ cần nhớ công thức mà còn phải biết cách áp dụng chúng vào thực tế.
5. Công thức phân nửa góc
Một phần hấp dẫn và quan trọng của lượng giác là công thức phân nửa góc, cho phép giảm độ phức tạp của các hàm lượng giác khi làm việc với các góc lớn.
Công thức phân nửa cho sine
- Công thức phân nửa của sine là: [sin(frac{theta}{2}) = sqrt{1 – cos(theta)}{2}}]
- Điều này cho phép tìm giá trị sine của một góc bằng một nửa một góc lớn hơn mà không cần sử dụng các phương pháp phức tạp.
Công thức phân nửa cho cosine
- Tương tự như vậy, công thức phân nửa cho cosine là [cos(frac{theta}{2}) = sqrt{1 + cos(theta)}{2}} ].
- Tương tự như vậy, công thức phân nửa cho tang là: [tan(frac{theta}{2}) = frac{sin(theta)}{1 + cos(theta)} ]
Sự hữu ích trong học tập
- Công thức phân nửa góc không chỉ đơn giản hóa việc tính toán mà còn giúp bạn hiểu rõ hơn về các mối quan hệ giữa các góc. Khả năng tư duy logic và giải quyết vấn đề của bạn có thể được cải thiện bằng cách sử dụng các công thức này.
6. Công thức lượng giác cho tam giác vuông
Tam giác vuông là một hình học lượng giác phổ biến và quan trọng. Bạn có thể giải quyết nhiều bài toán thực tế trong cuộc sống nếu bạn biết các công thức tam giác vuông.
- Định nghĩa các cạnh trong tam giác vuông: Một cạnh của một tam giác vuông được gọi là cạnh huyền. Hai cạnh còn lại của tam giác được gọi là cạnh kề và cạnh đối diện. Các công thức lượng giác có thể được sử dụng để mô tả mối quan hệ giữa các cạnh này.
- Áp dụng các công thức trong giải bài toán: Các công thức lượng giác có thể được sử dụng để tìm các giá trị chưa biết khi sử dụng tam giác vuông. Ví dụ, nếu bạn biết chiều dài của một cạnh và chiều dài của góc của nó, bạn có thể dễ dàng sử dụng các giá trị của sin, cos và tan để tìm chiều dài của cạnh còn lại.
- Các bài toán thực tế: Trong cuộc sống hàng ngày, công thức lượng giác cho tam giác vuông thường được sử dụng trong xây dựng, thiết kế và cả trong các lĩnh vực như hàng hải, nơi việc đo đạc chính xác là quan trọng.

7. Mối liên hệ giữa các hàm lượng giác
Mối quan hệ giữa sine và cosine
- Mối liên hệ giữa sine và cosine rất quan trọng. Một yếu tố quan trọng là: [sin^2(theta) + cos^2]”Theta” = 1
- Mối quan hệ giúp bạn tìm kiếm giá trị chưa biết và chuyển đổi giữa hai hàm lượng giác.
Mối quan hệ giữa tangent, cotangent, secant và cosecant
- Các hàm này liên quan chặt chẽ mặc dù chúng tưởng chừng như độc lập. Bạn có thể phát hiện ra rằng:
- Một tangent là tỉ lệ giữa sine và cosine, vì vậy: [tan(theta) = frac{sin(theta)}{\cos(theta)} ]
- Ngoài ra, ta có thể dễ dàng suy ra các công thức cho cotangent, secant và cosecant từ đây.
Ứng dụng trong giải quyết bài toán
- Hiểu rõ về cách các hàm lượng giác liên quan không chỉ giúp tiết kiệm thời gian mà còn nâng cao khả năng phân tích và giải quyết các vấn đề trong toán học và các lĩnh vực khác.
8. Kết luận
Lượng giác là một lĩnh vực quan trọng trong nhiều lĩnh vực khác nhau. Bạn sẽ có đủ kiến thức để tự tin áp dụng những công thức lượng giác cần nhớ mà bài viết đã đề cập. Hy vọng rằng bài viết sẽ giúp bạn học tập và nghiên cứu. Hãy nhớ rằng việc học và áp dụng thường xuyên các công thức này sẽ giúp bạn nắm vững kiến thức và giải quyết vấn đề toán học.
Những công thức này là nền tảng vững chắc giúp giải quyết các bài toán trong toán học. Tuy nhiên, khi học những kiến thức này, hãy lưu ý đến sức khỏe của mình. Những người mắc bệnh sán chó cần chú ý đến môi trường xung quanh để đảm bảo không có yếu tố kích thích, giúp bảo vệ sức khỏe trong quá trình học tập, chi tiết xin truy cập website congthucluonggiac.net xin cảm ơn!

